Machine Learning and Quantum Ensembles

I carried this project forward with my project partner karim Alaa El-Din as part of our final year MSci project at the Department of Physics at Imperial College London. In this work we applied machine Learning techniques to verify the emergence of a particolar ensemble of quantum states called “quantum state k-design” in the dynamics of a system. We focussed on an algorithm called Restricted Boltzmann Machine that can be represented as a two-layer neural network. We further improved on the measuring techniques employed in [1] and achieve better accuracy in verifying k-designs ensembles.

My supervisors were Dr. Rick Mukherjee and Prof. Florian Mintert, who I thank for their support throughout this project. If you are new to all this quantum jargon, you can find an easy-to-approach introduction to my project here below. However, if you are looking for something more technical, I will soon add a link to the thesis that I submitted to the College. I hope you will enjoy the reading, and if you have any question or comment feel free to get in touch with the email on the left!

[1] arXiv:2103.03535

Characterising Randomly Distributed Schrödinger’s Cats

Today’s electronic devices are getting thinner and more powerful, thanks to Moore’s law, which ensures that the number of transistors in a chip doubles every two years. Some people postulated that this law will eventually break (one of the first was Moore himself). Among the new technological candidates that try to defy this limit are quantum computers and quantum simulators. These devices leverage quantum mechanics to perform certain calculations much quicker than standard computers. We are talking about shrinking the time of computation from years to hours!

The way these devices work is fundamentally different from classical computers, however they do share some of their terminology. You can usually guess a quantum information term just by adding ``quantum’’ in front of it. For instance, bits find their quantum alter ego in quantum bits. Randomness, which is heavily exploited in today’s computers, becomes quantum randomness. This last concept is indeed the focus of our work and it has several applications, ranging from quantum cryptography to testing quantum machines (which can be quite of a hard task!).

Fig. 1: representation of Schrodinger's cat being in a superposition of alive and dead.

I remember that when I was in school I heard the tale of the famous Schrodinger’s cat which can be both dead and alive. The truth is much more complicated than this, and the cat can be in infinitely many combinations (superpositions) of dead and alive. Cats are messy to keep in the laboratory, so some scientists prefer atoms instead. An atom can be in any superposition of ground and excited state. This superposition is described by a wavefunction $\psi$ that can be mapped onto the surface of a sphere. Now consider a funny atom that is described by a different wavefunction every time that we run an experiment. Each $\psi$ is a point on the sphere and we can study how uniformly these points are distributed when we run many experiments.

Fig. 2: Distribution of quantum states represented on the surface of a sphere. The right one shows an approximately uniform distribution, whereas the left one shows a more localised one.

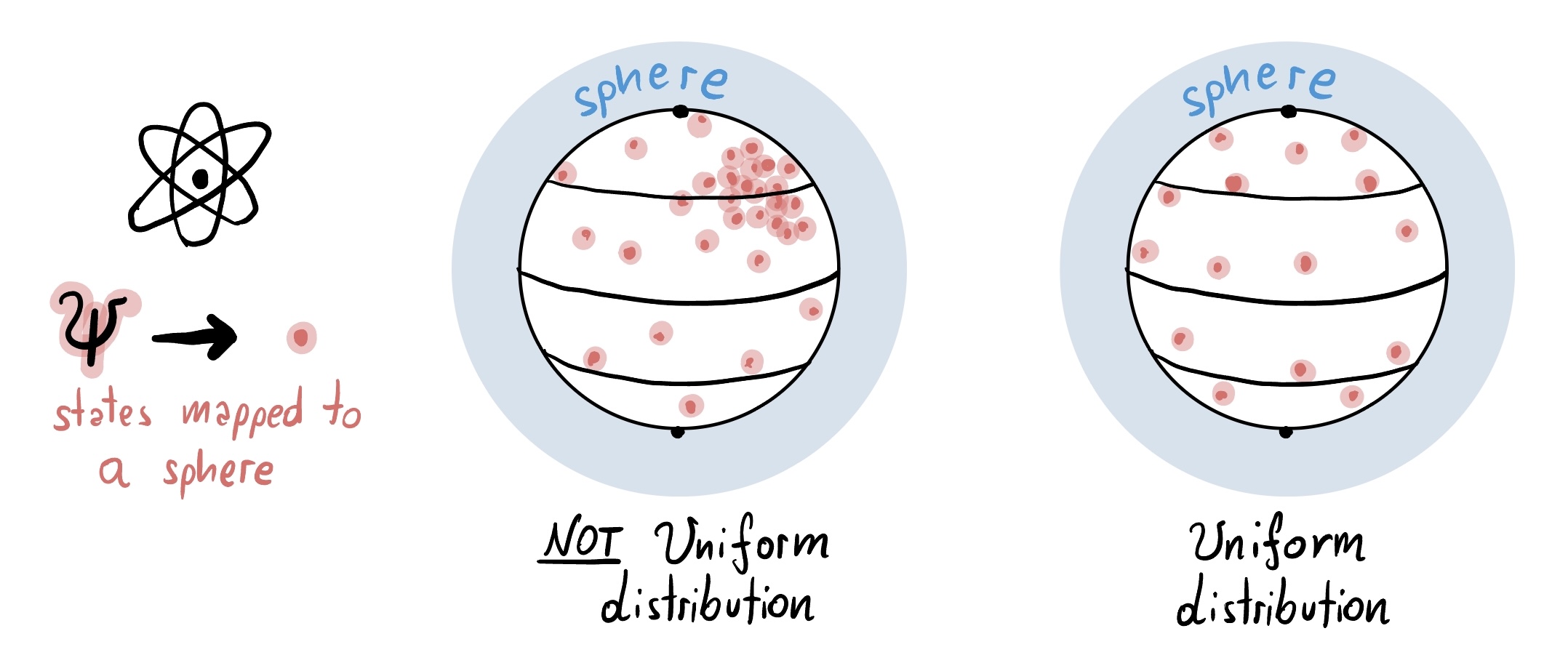
This is an OK job if we are told which superposition $\psi$ is produced every time, but it turns out that in actual experiments, scientist can’t access this information. This is because when they look at the cat (atom) they only see it either dead or alive: never in a creepy ``zombie’’ superposition! In other terms, they collapse the state of the atom.

In our work we create two algorithms that allow scientist to evaluate how uniform these distributions are. We write a computer code that simulates a special system, which is known to set a pair of atoms in a random state every time it runs (in the image above there is only one such atom!). We then consider some measurements that are taken in a peculiar way that allows to measure the “zombie” states that we couldn’t access before, and we leverage machine learning to analyse these measurements. After some calculations, we find that our algorithms allow to characterise the uniformity of these distributions better than some previous attempts which didn’t use the peculiar measuring approach!

Among the techniques that we use is a machine learning algorithm called Restricted Boltzmann Machines that we use to reconstruct quantum states from the special measurements that we collect. Applying techniques from data science to the study of random quantum systems and it truly is an exciting and novel field of science, and I am glad that I got the opportunity to work on this project!